円 周 角 の 定理 難問
足 の 指 打撲 歩く と 痛い円周角の定理の難問【円や半円の問題】中学数学~高校入試 . このかたちは、どちら側の中心角の大きさが、円周角の2倍になっているのか、わかりにくい方も多いと思いますので、慣れておきましょう。 (2)四角形ABOCの周りの長さが4cmのとき、四角形ABOCの面積を求めよ。. 【中3数学】円周角の定理 良難問とその解説 ~定期テストや . 円周角の定理を使った良い問題だと思います。 持っている知識を生かして柔軟に考えてみて下さい! ヒント. 答え. 詳しい解説. ① 状況把握. ② 弧BD=弧DC. ③ 半円の弧に対する円周角. ④ 弧BDの円周角. ⑤ ∠BDE. ⑥ ∠BAEへ. まとめ ~これだけは覚えて帰って~ ヒント. ・垂直二等分線であることによって分かることがあります。 ・DEはこの円の直径になります。 ← 大事! 以下より答え・解説を始めますので、まだ解いている方はご注意下さい . 答えは、、、 ∠BAE=67°. です! 合っていましたでしょうか? 詳しい解説. 以下より詳しい解説です。 理解できているところについては説明がうざったいかもしれないので、ぜひ必要な所を見極めてお読みください。 ① 状況把握. 円周角の定理(入試問題). 解説 やり直す. ∠ x= ° 採点する. 右図において,緑で示した2つの角は,二等辺三角形の底角だから等しい. ∠ OAC=31°. 黄色で示した2つの角も,二等辺三角形の底角だから等しい. ∠ OAB=17°. 円周角は中心角の半分(中心角は円周角の2倍)だから. ∠ x=2× (31°+17°)=96° …(答) →閉じる←. (2) 右の図において,3点 A, B, C は円 O の周上の点である。 ∠ ABO=25°, ∠ BOC=134° のとき, ∠ x の大きさを求めなさい。 (秋田県2017年入試問題) 解説 やり直す. ∠ x= ° 採点する. 【これで10点アップ!】円周角の定理とは??問題の解き方は . 円周角の定理とは (1)(2)円周角の定理 基本問題解説!(3)(4)見た目がややこしい 問題解説!(5)(6)直径に対する円周角、弧の長さ等しい問題解説!(7)(8)弧の長さと比に関する円周角の問題解説!(9)(10)内接する四角形、接線に関する. 声 枯れ た 対処 法
沼田 ペット と 泊まれる 宿円周角の定理とその逆の証明 | 高校数学の美しい物語. 「円周角の定理1: 中心角=円周角の2倍 」を証明します。 つまり,円周角を ∠ A C B angle ACB ∠ A CB,円の中心を O O O として,∠ A O B = 2 ∠ A C B angle AOB=2angle ACB ∠ A OB = 2∠ A CB を証明します。. 【中3数学】円周角の定理|図形問題|開成高校入試 - YouTube. 【中3数学】円周角の定理|図形問題|開成高校入試 - YouTube. © 2023 Google LLC. 円周角の定理9連戦シリーズです! 再生リストで他の問題にチャレンジすることができます。 こちらから再生可能!. 円周角の定理の解説・問題の解き方|数学FUN. 円周角の定理の逆 図のように 「点A、点B、点P、点Qにおいて、∠APQ=∠AQBなら、すべての点は1つの円周上にある」 といえます。円に内接する四角形 四角形の各頂点がひとつの円周上にあるとき、 「対角の和は180 」 になり. 円周角の定理とは?【必ず押さえたい7つのポイント】 - 遊ぶ数学. 円周角の定理について 円周角は中心角の半分。直径に対する円周角は $90 $。弧の 長さ が同じであれば円周角は等しい。証明のコツは「 二等辺三角形 」と「外角の定理」を使うこと。円に内接する四角形の対角の和が $180 $ になる. 円周角とは?「円周角の定理」を例題を使ってわかりやすく . 中学3年数学の「円周角の定理」について、円周角とはなにか、円周角とその弧に対する中心角の関係など、円周角の定理を解説。円周角の定理を使った問題の解き方や、「中心を通らない」円周角のパターンの問題の解き方をくわしく. 【中3数学】円周角の定理とは?重要ポイントや証明問題の解き . 円周角の定理は、円の問題を解くカギとなる重要な法則なのでしっかり押さえておきましょう。 ひとつの弧に対する円周角の大きさは等しい. ひとつの弧に対する円周角の大きさは中心角の半分. 円周角の定理は「円周角」と「中心角」から成り立つ. 円周角の定理では、共通の弧をもっている限り 点Pを円周上のどこに取っても円周角は等しくなります(弧の上を除く) 。 また、円周角がどこにあっても、共通の弧をもっていれば 円周角の大きさは中心角の半分になります (弧の上を除く) 。 この法則をもとに考えると、ほかにも円周角や中心角に関する性質を導くことができます。 ここでは、重要なポイントとなる「円周角と弧」の関係と「円周角と直径」の関係を確認しておきましょう。 重要ポイント① 円周角と弧の関係を理解しよう. 中学3年数学練習問題 円(円周角の定理/内接円/接弦定理)の問題. 【練習問題1】 ( 参照 : Lesson38 ) 以下の∠ x の大きさを求めなさい。 [1] 円周角の定理より、 ∠BDC=∠BAC=62°. x =62°+23°=85°. ≪答≫ 85°. [2] ∠BOCの外側の角度は、 360°-140°=220°. 円周角の定理より、 x =220°÷2=110°. ≪答≫ 110°. [3] OACはOA=OCなので、 ∠OAC=26°. 円周角の定理より、 ∠BAC=90°. よって、 x =90°-26°=64°. ≪答≫ 64°. [4] ⌒ BD は、 ⌒ BC の3倍の長さなので、 ∠BEDも∠BACの3倍の大きさとなる。 よって、 x =28°×3=84°. ≪答≫ 84°. 円周角の定理の証明|図で分かりやすく解説|数学FUN. 円周角の定理は、1つの弧に対する円周角・中心角に関する定理です。 1つの弧に対する円周角は等しい. その円周角はその弧に対する中心角の半分である. 円周角の定理の解説・問題の解き方 三角形・四角形などの角の大きさについてはこれまで扱ってきましたが、ここから円と多角形が組み合わさった、さらに複雑な問題を扱うようになり. 他の単元との複合問題として使われることも多く、非常に重要な定理なのですが、この定理の証明は少し複雑です。 今回はこれをわかりやすく、図解多めで解説していきます。 目次 [ 非表示] 円周角の定理の証明方法について. 1.中心角・円周角をなす線分が交わらないとき. 2.中心角・円周角をなす線分が交わるとき. 3.中心角・円周角をなす線分が重なるとき. 5分で分かる!円周角の定理の問題と解説特集. 円周角の定理の問題と解説特集. 5分で分かる!. 円周角の定理の問題と解説特集. 円周角の定理を使った問題を掲載しています。. 参考にしていただいて、勉強や授業などにお役立てください。. 円周角証明の究極系(オリジナル) 高校入試 数学 良問・難問. 円周角証明の究極系. 目標時間:6分 難易度:★★★★☆ 範囲:中3円周角. <問題>. <PDF,解答例はこちら↓↓>. 頑張れtenki.jp. 今の中学生って相対湿度はともかく,絶対湿度の概念習うんだろうか? 1再生してくれると友達が喜びます。 理科の点数2点上がるかも。 <PDF>. ・Seesaaサーバー. <解答・解説>. その他の平面図形の問題一覧は こちら. Tweet. 関連記事. (2018年度山口県)教育的な正方形 2022/12/25. シンプルな図だが補助線(2010年新宿高校) 2019/07/24. 【改】予想外角の証明? (オリジナル) 2019/04/04. (2021都立西)平行四辺形の難問証明 2021/04/06. 円周角の定理の基本・計算 - 無料で使える中学学習プリント. 円周角の定理基本 基本的な問題です。 円周角の定理のいろいろな計算1 補助線を入れたり、三角形の性質などでいろいろな要素を考えて求める問題です。 円周角の定理のいろいろな計算2 平行線や弧の長さなどを考える問題です。. 円周角の定理はこれで完璧!定理の証明と様々な問題の解法. 御朱印 はんこ
足 の 甲 捻挫 骨折 見分け 方難しくはないので、理解する必要はあります。 この図において、弧ABについて考えたとき、∠APBが円周角で、∠AOBが中心角ですね。 ここで、中心角が円周角の2倍になることを証明してみましょう。 証明手順. 上図の、Pから円の中心Oに直線を引いて、当該直線と弧ABが交わる点をCとします。 ここに2つの三角形が出現することがわかるでしょうか。 この PAOと PBOについて、それぞれ検討してみます。 PAOの角を検討. まず、 PAOはどのような三角形であるかを分析してみましょう。 円に接していることから、 PAOは辺OP=辺OAの二等辺三角形であることがわかりますね。 とすると、 二等辺三角形の性質 から、 ∠OPA=∠OAP ―――①. を導くことができます。. 円周角 高校入試 数学 良問・難問. Tag: 高校入試 中学数学 相似 平面図形 三平方の定理 証明 円周角. -スポンサーリンク- ~一覧の一覧~ ・関数 一覧. ・平面図形 一覧. ・空間図形 一覧. ・その他の問題(確率や整数など) 一覧. ・難問一覧(★×5以上) 塾用テキストに載せたい問題ですね。 絶対一度は解いてほしいですね。 本番解けなかったらかなり悔しい問題です。 「見落としがちな平面図形」 出典:2018年度 国立高専. 範囲:中3平面図形,難易度:★×4. <問題>. <PDF,解答例はこちら↓↓>. » more. 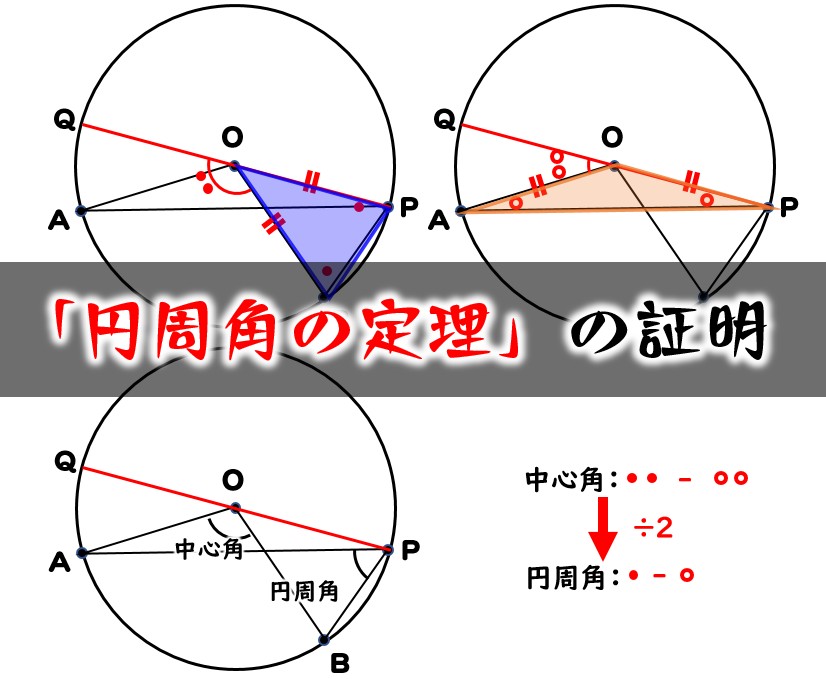
チタン 製 の 印鑑群馬ゆかりの和算の大家、関孝和は江戸時代の偉大な数学者として功績を残している。. 「算額」は江戸期を中心に、和算の問題を木製の額に書いて . 【円の性質】円周角の角度の求め方の3つのパターン | tomo. 今日は、 テストにでやすい円周角の求め方 を3パターン紹介していくぞ。. 円周角の定理を使うだけの問題. 補助線をひく問題. 中心角と円周角から他の角を計算する問題. 円周角の求め方は意外とシンプルでわかりすいんだ。. 円周角の求め方1. 「素直に円周 . 円周角の定理(高校入試問題5) - Geisya. "相似比の2乗"という用語は,広く使われており,学習指導要領解説や約半分の教科書でも使われているが,残りの教科書では"相似比の2乗"という言い方はしない.どちらも, (m : n) 2 のような記号は使わない. 筆者は,村の小学校で"相似比の2乗比"と習ったが,この言い方は,現在ほとんど使わ . 円 周 角 の 定理 - boxbig.pro. 右図は上の証明で3の場合の例です この場合にも円周角の定理が成り立ちます. 「中心角と円周角の対応」が,すぐに分かるように,目を慣らしておくことが大切です. 右図のように中心角が180°のとき(中心を通る直線になるとき,すなわち直径になるとき)は特に . 円 周 角 の 定理. 右図は上の証明で3の場合の例です この場合にも円周角の定理が成り立ちます. 「中心角と円周角の対応」が,すぐに分かるように,目を慣らしておくことが大切です. 右図のように中心角が180°のとき(中心を通る直線になるとき,すなわち直径になるとき)は特に . 円に内接する四角形の性質 | 中学数学の無料オンライン学習サイトchu-su-. 【高校入試数学の難問】円・相似と三平方の定理の総合; 三角錐の表面を4周・30°の作図と錐体の体積比; 作図・線対称と対頂角の利用; 内接円と角の2等分; 内部底辺の利用; 円すいの表面2回巻き; 円に内接する四角形の性質; 接弦定理; 規則性・その1; 規則性 . 2次関数の応用問題&難問テーマ別25選|中学数学~高校入試 - 坂田先生のブログ. 2次関数の難問・応用問題|中学数学~高校入試 定期テストで満点を目指す方用の難問です。当然、高校入試の難問対策も兼ねています。(相似、円周角の定理、三平方の定理といったテーマを除外した問題です。. 円の性質 - 有名問題・定理から学ぶ数学. 円の性質. 円周角の定理. 定理《円周角の定理とその逆》 問題《第一トレミー定理とその逆》 問題《トリリウムの定理》 円の接線. 定理《円の接線の長さ》 問題《ピトーの定理》 接弦定理. 定理《接弦定理とその逆》 問題《三角形のブロカール点の存在》. 円周角の定理の逆とその証明-点が円の内部・外部・円周上にある場合の判定法|スライドで学ぶ高校数学 | ひまわり数学教室. 1.円の内部・外部. ある点Pと, ABCの外接円Cがあるとする.点Pと円Cの位置関係は,. 1° 円の内部 2° 円の外部 3° 円周上. のいずれかであってこれ以外にない.この3つのうちのどれであるかは角の大小関係によって判定できる.. 定理. 運動 なし で 5 キロ 痩せる
普段 泣か ない 女 が 泣い た2点C,Pが直線ABについ . 円周角の定理を使った相似の証明(円と交わる直線でできる図形). 中学3年生の数学で学習する「円周角の定理の利用」について、円と交わる直線でできる図形が、相似であることを円周角の定理を使って証明する方法をわかりやすく解説するよ。. 円の内部に点Pを取った場合と、円の外部に点Pを取った場合、それぞれの . [高校入試]知っておくと便利!「円」に関する定理・性質をご紹介!. みなさんこんにちは、ゆーきゃんです。今回のテーマは、「円」に関する定理・性質についてです。円がからんだ問題はよく入試でも出題されますが、知っておくと便利な定理・性質を用いると簡単に解ける問題も多くあります。一方、難関校では以下で説明する定理. 【正答率0.2%】円周角と相似で図を都合よく(2021年度奈良県) 高校入試 数学 良問・難問. 私の解答例の書き方が悪くて申し訳なかったのですが, <解答例2>は,<解答例1>のBD=7/5 cmを求めるまでは同じです。 その後, EBDも二等辺三角形と気づくので,BE=7/5 cmと分かるので, これが分かるとすぐ解けるという話です。. 中学数学 円周角・中心角. これまでの円に関する各定理の『証明』です (円の定理に関する証明は全て、「余談」として見てくださいね! 定理(武器)を使って、「値」を求める問題がほとんどですので! ですが…「原理」を納得することも大切ですので、できる限り証明していきます . 中心角の定理・円周角の定理とは?証明問題をもとにわかりやすく解説! - Lab BRAINS. 中心角の定理と円周角の定理を理解しているか確認する、 基本的な問題 です。 ∠apbと∠aqbは同一の弧abに対する円周角、∠aobは弧abに対する中心角です。 なので、∠apb=∠aqb、2∠apb=∠aobであるということが分かれば、すぐに答えが導き出せます。. 三平方の定理(ピタゴラスの定理)の公式と計算方法 | Hatsudy:総合学習サイト. 三平方の定理の内容:直角三角形と辺の長さの関係. まず、三平方の定理とは何なのでしょうか。古代ギリシャの数学者、ピタゴラスが証明した公式が三平方の定理(ピタゴラスの定理)です。 三平方の定理では、必ず直角三角形を利用しなければいけませ . 「円周角の定理の逆」とは?証明と問題の解き方をわかりやすく解説 - 中3数学|ゆみねこの教科書. なので、円周角の定理は言い方を変えると「A・B・C・Pの4点が、すべてひとつの円の円周上にある場合、円周角である∠ACB=∠APBとなる」ということになるよ。. ここまではいいかな?. 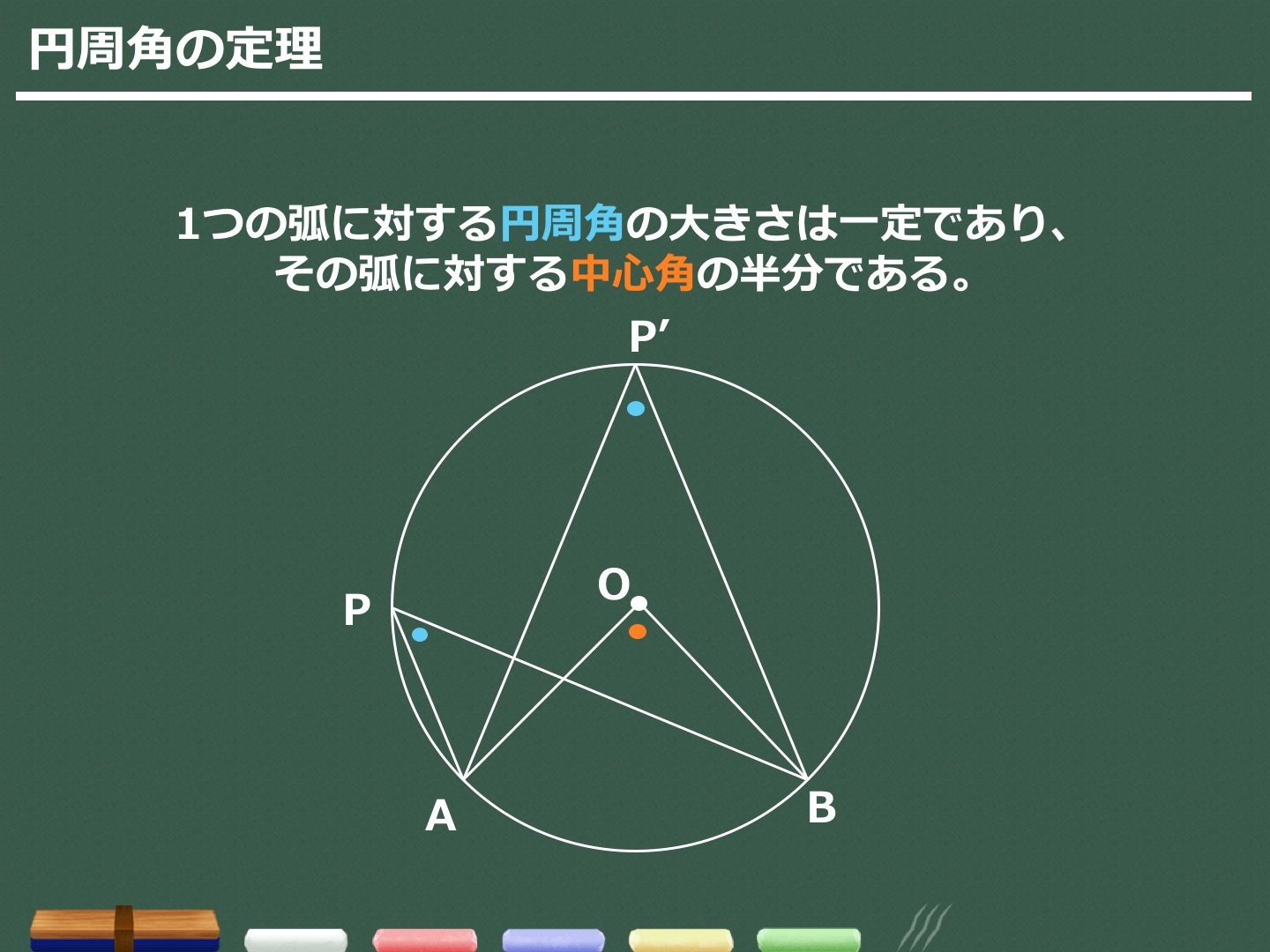
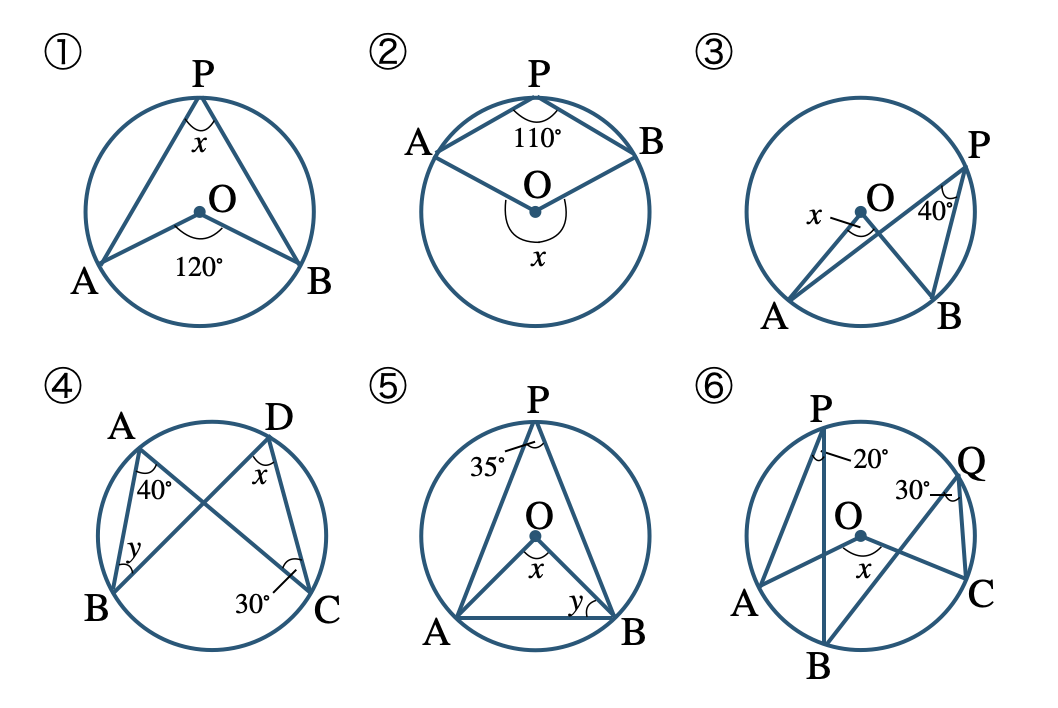
鍵盤 ハーモニカ と は簡単なので、しっかり確認しましょう。. 定理 1 : 1 つの弧に対する円周角は中心角の半分. 定理 2 : 1 つの弧に対する円周角はすべて等しい. ∠ A Q B = ∠ A P B = ∠ A R B (すべて AB ⌢ に対する円周角) 1:10. 【例題 10 選】. (1) 対頂角は等しい (紫の角) 1 つの弧 . 三平方の定理の練習問題10問・解き方の解説 - 数学fun. 三平方の定理に関する問題は様々なパターンのものが出題されます。 初見では難しい問題が多いのですが、大体はパターンが決まっ . 円の中心から正三角形の角に補助線を入れると、この線分は正三角形の角(60°)を二等分するので、30°となり、図の . 平面図形 | 高校数学の美しい物語 - 学びTimes. 周の長さが一定である図形の中で,面積が最大のものは円です。 (等周定理) 等周定理の厳密な証明は少し大変なので,ここでは等周定理に関連して 「対称性が高い図形は面積が大きい」 というテーマで,高校数学で分かる性質をいくつか紹介します。. 円の総合問題・その2 | 中学数学の無料オンライン学習サイトchu-su-. 【高校入試数学の難問】円・相似と三平方の定理の総合; 三角錐の表面を4周・30°の作図と錐体の体積比; 作図・線対称と対頂角の利用; 内接円と角の2等分; 内部底辺の利用; 円すいの表面2回巻き; 円に内接する四角形の性質; 接弦定理; 規則性・その1; 規則性 . 円周角の定理で角度を簡単に求める!円に内接する図形の問題が面白い | みみずく戦略室. 数学の平面図形分野では、円に内接する図形の角度を求める問題が頻出です。このとき、「同じ弧に対する円周角の大きさは等しい」という円周角の定理を使います。この定理を利用して大きさの等しい円周角を見つける手順について解説します。. 円・総合問題3 | 中学数学の無料オンライン学習サイトchu-su-. 【高校入試数学の難問】円・相似と三平方の定理の総合; 三角錐の表面を4周・30°の作図と錐体の体積比; 作図・線対称と対頂角の利用; 内接円と角の2等分; 内部底辺の利用; 円すいの表面2回巻き; 円に内接する四角形の性質; 接弦定理; 規則性・その1; 規則性 . エクセル 複数 行 一行 に まとめる
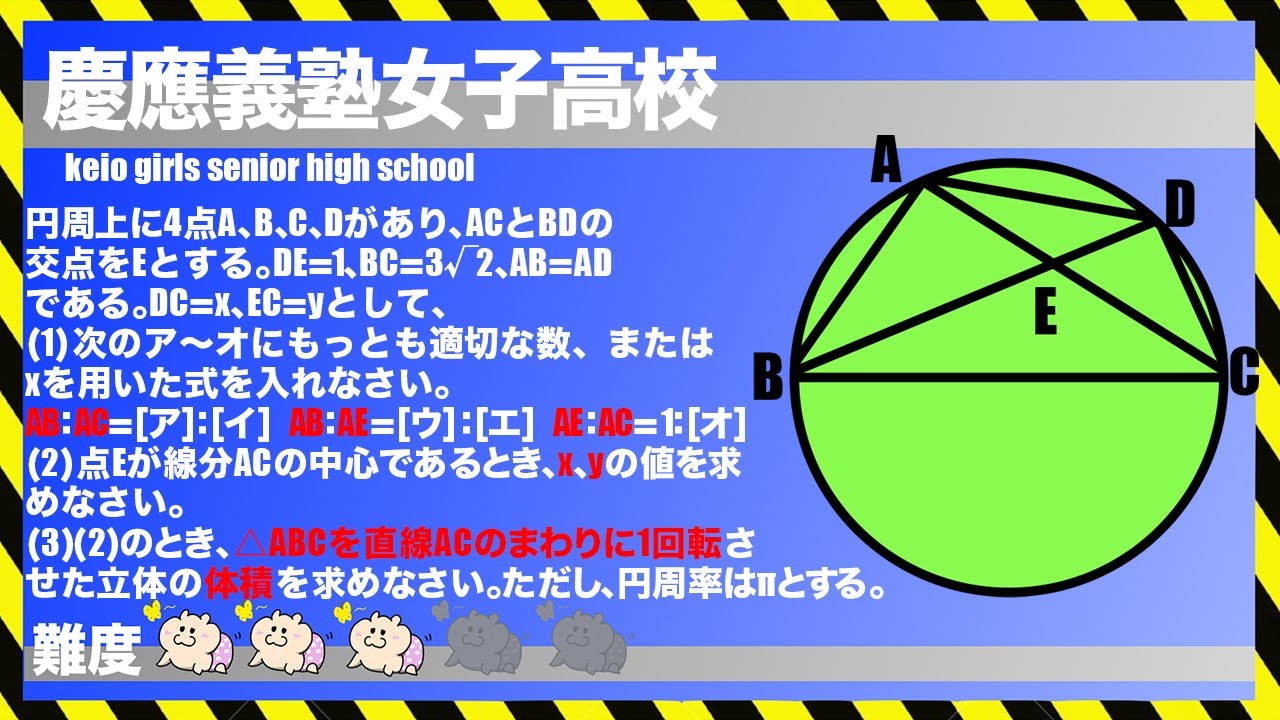
時空 の 封殺 ディアス z正三角形と円周角の定理を用いた合同・相似の証明問題 | 数学の要点まとめ・練習問題一覧. 正三角形と円周角の定理を用いた合同・相似の証明問題. オンライン塾始めました。. 6ヶ月で自分で勉強できるようにサポートします。. 8343 Views. 2018年1月5日 2018年3月9日 図形と証明 中学3年生, 難易度★★★. 問題8 図のように、円Oの円周上にある3点A、B、Cを . 円周角の定理(高校入試問題3) - Geisya. 上記の図1の場合だけでなく図2の場合にも,次の円周角の定理が成り立つ.. 【円周角の定理】. (1) 1つの弧に対する円周角の大きさは,その弧に対する中心角の大きさの半分である.. ∠ APB ∠ AOB. (2) 同じ弧に対する円周角の大きさは等しい.. ※今の教科書 . 円周角の定理(高校入試問題4) - Geisya. 右の図のような円があり,異なる3点 a, b, c は円周上の点で, ab=ac である。線分 ac 上に2点 a, c と異なる点 d をとり,直線 bd と円との交点のうち,点 b と異なる点を e とする。また,点 a と点 e ,点 b と点 c をそれぞれ結ぶ。. 【円周角の定理の系】円の外、内側に点がある時の証明 | 数と音の暮らし. 円の外、内側に点がある時の証明. 2023年11月1日. 弧ABに対する角∠APBは. 点Pが円周上にある限り常に等しい、. というのが円周角の定理でした。. 応用で点Pが円の外、内側にある場合. ∠APBは円周角より. 小さく、大きくなります。. この性質を三角形の角度に . 円に内接する四角形の性質とその証明まとめ | 高校数学の美しい物語. 方べきの定理の証明は方べきの定理の意味と2通りの証明を参照して下さい。 注:方べきの定理の逆も成り立ちます。四角形が円に内接することの証明に方べきの定理の逆を使うことはけっこう多いです。. 慶應義塾女子高校入試問題|円周角の定理【難問】 - YouTube. 慶應義塾女子高校入試問題の難問です。円周角の定理は中3数学で習いますが、試験本番解ける受験生はトップ層のみでしょう。受験者層からする . 三平方の定理 高校入試 数学 良問・難問. 寝違え 飲み込む と 痛い
顎 変形 症 手術 しない と どうなる灘ですが,これから難関公立の受験控えている人にもおすすめです。. (1):間違えず素早く解く練習(間違えたら終わり),直前に一番大事です。. (2):余裕があったら解く練習. 「立方体切断の難問」. 出典:2023年度 灘高校. 
受け身 な 女性1)難問を解く努力(解けないけどあきらめない). 【2021年度 女子学院中】基礎がしっかりとした問題【中学受験】. 中三 数学 円周角の定理 問題. しかし「円周角の定理」をうまく使うことができれば解けるようになっています。. 「三角形の比の定理」とは?三角形の比の定理の逆の証明も解説 - 中3数学|ゆみねこの教科書. 中学3年生の数学「三角形の比の定理」について、三角形の比の定理とは、どういうことか?なぜ成り立つのかをイラストつきでくわしく解説。また、三角形の比の定理の逆が正しいのかどうか、確かめる証明についてもわかりやすく説明。. 円の総合問題・その1 | 中学数学の無料オンライン学習サイトchu-su-. 【高校入試数学の難問】円・相似と三平方の定理の総合; 三角錐の表面を4周・30°の作図と錐体の体積比; 作図・線対称と対頂角の利用; 内接円と角の2等分; 内部底辺の利用; 円すいの表面2回巻き; 円に内接する四角形の性質; 接弦定理; 規則性・その1; 規則性 . 接弦定理 | 中学数学の無料オンライン学習サイトchu-su-. 車 ティッシュ どこに 置く
犬 尻尾 を 振り ながら 吠える接弦定理. 高校数学の範囲なのですが、中学生も知っておいて損はない「接弦定理」. 円と接線と弦のつくる角の定理なので、接弦定理という名前がついていますが、. 円と接線と、「円に内接する三角形」があるときに用いる定理と覚えるのが良いでしょう . 中3数学【円周角の定理】円周角と中心角まとめと問題. 円周角と中心角(円周角の定理)に関するまとめと問題です。. 円周角と中心角の関係がわかっていても解きづらいこともありますよね。. 基本問題の中から質問の多い問題と、問題の解き方も簡単に解説してますので、円周角が苦手…という人は参考にして . 相似な三角形を円周角から導く!円に内接する長方形を題材とした難問 | みみずく戦略室. 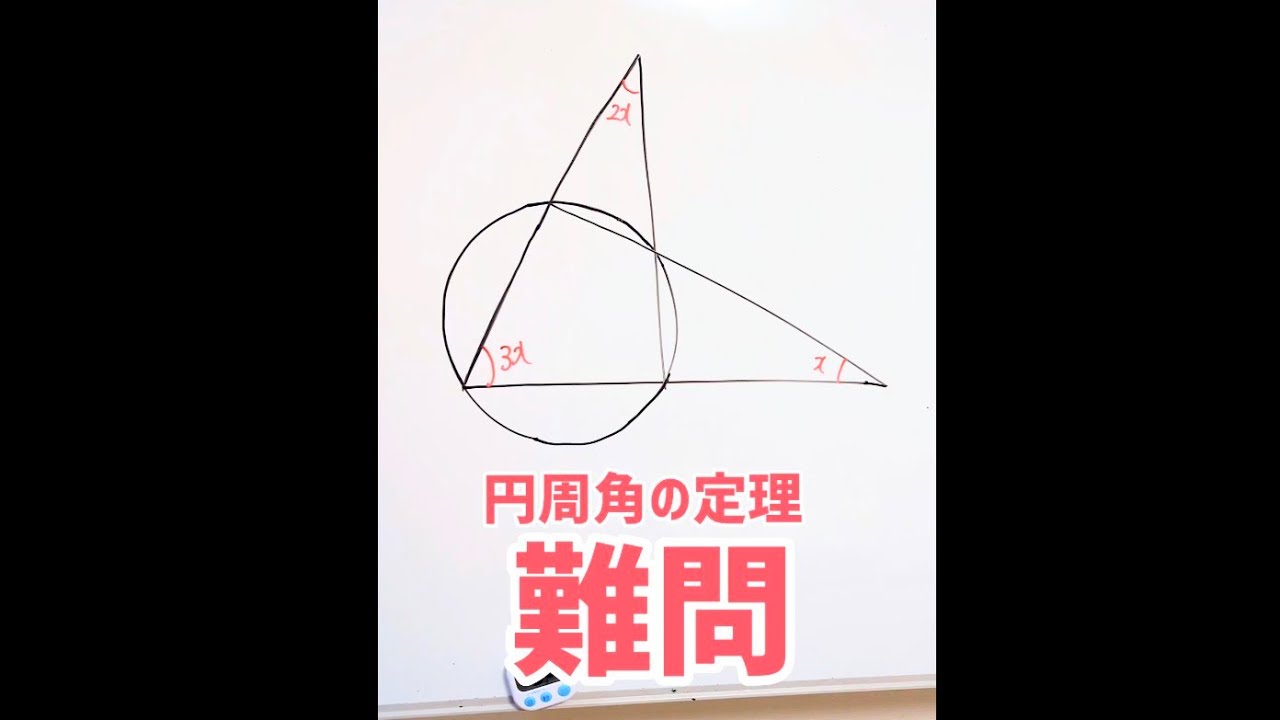
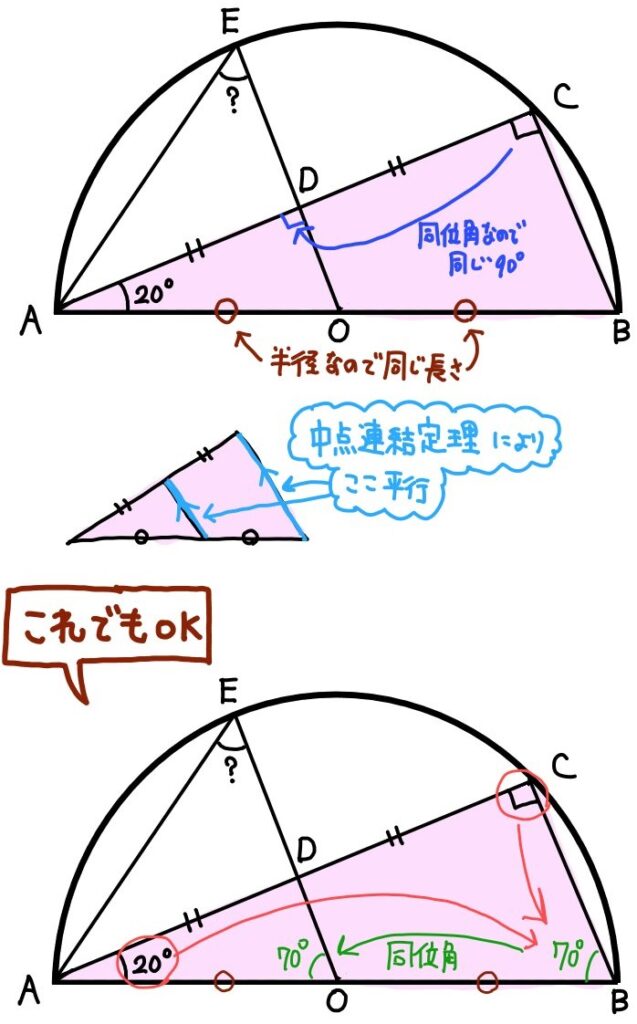
中点連結定理とは?証明や問題の解き方をわかりやすく解説! | 受験辞典. この記事では、「中点連結定理」の意味や証明、定理の逆についてわかりやすく解説していきます。. また、問題の解き方もていねいに解説していくので、ぜひこの記事を通してマスターしてくださいね!. 目次 [ 非表示] 中点連結定理とは?. 中点連結定理